Conjutos de Pares Ordenados

PARES ORDENADOS

Según el matemático alemán Georg Cantor (1845-1918) en su teoría matemática define un conjunto de par ordenado un conjunto de una colección de objetos bien definidos. Los elementos de un conjunto pueden ser abstractos, como el conjunto de los números primos menores que 10, u objetos concretos como el conjunto de todas las monedas que tenga en sus bolsillos.

Para indagar que son los pares ordenados debemos saber conceptos básicos que nos llevaran a la comprensión de dicho tema como : conjuntos , elementos, pares .

Conjuntos:un conjunto es una colección de elementos considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser las siguientes: personas, números, colores, letras, figuras, etc.

Ejemplo: el conjunto de los colores del arcoíris es:

AI = {Rojo, Naranja, Amarillo, Verde, Azul, Añil, Violeta}

Un conjunto suele definirse mediante una propiedad que todos sus elementos poseen. Por ejemplo, para los números naturales, si se considera la propiedad de ser un número primo, el conjunto de los números primos es:

P = {2, 3, 5, 7, 11, 13, ...}

Elementos:  Un elemento (o miembro) pertenece al conjunto si esta definido como incluido de algún modo dentro de el.

Pares: Un grupo de pares tenemos que decir que pares es una palabra que abarca varios significado , por lo normal es de las palabras que cuando se usa es decir en que oración lo estas usando.

En matemáticas, un número par es un número entero que se puede escribir de la forma: 2k (es decir, divisible de manera entera entre 2), donde k es un entero (los números pares son los múltiplos del número 2). 

De esta manera los pares ordenados son muy utilizados cuando graficamos una función matemática en el sistema de coordenadas cartesianas, y muy útiles para visualizar el comportamiento de las ecuaciones y los mapeos.

Casi todo grado universitario o de colegio, y todo curso secundario en matemáticas requieren aprender a dibujar y graficar funciones matemáticas. No importa si usted está tomando cursos en línea (también llamado e-learning), aprendizaje presencial, o una mezcla de ambos métodos.

Desde simples gráficos lineales, hasta funciones parabólicas e incluso curvas trigonométricas, los pares ordenados son necesarios y utilizados en todos los campos de la ciencia y la tecnología.

Es tan fácil trazar puntos en el sistema de coordenadas cartesianas que muchas veces no nos molestamos encontrar los fundamentos matemáticos de los pares ordenados.

Cuando hablamos de par ordenado , nos estamos refiriendo a dos números, o figuras, encerrados en un paréntesis.

Su representación general es:

(  a , b )

Respecto a esto, podemos preguntarnos ¿cómo se obtiene un par ordenado?, ¿para qué sirve un par ordenado?

Un par ordenado se puede obtener desarrollando una función o realizando la operación llamada producto cartesiano .

Como consecuencia, un par ordenado sirve para representar un subconjunto del producto cartesiano entre dos conjuntos, un punto en un plano cartesiano o bien  una razón o una función.

PRODUCTO CARTESIANO

Cada par ordenado es una combinación entre elementos del conjunto A y elementos del conjunto B . Siempre el primer elemento pertenece al primer conjunto y el segundo elemento al segundo conjunto pero no al revés porque su representación no es conmutativa , es decir, no se puede alterar el orden.

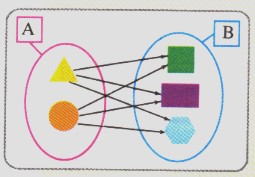Observa en el recuadro superior los conjuntos A y B y las combinaciones que se pueden hacer entre los elementos de ambos conjuntos.

Estas combinaciones se pueden representar mediante pares ordenados, tal como se indican en la siguiente tabla.

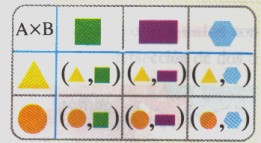PLANO CARTESIANO

Todo par ordenado escrito con números representa un punto del plano, donde la primera componente (el primer número) recibe el nombre de abscisa (eje x) y la segunda componente recibe el nombre de ordenada (eje y).

Los pares ordenados (3,  4) y (5,  2) están representados en el siguiente plano cartesiano (gráfico):

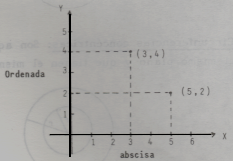
Abscisa : X

Ordenada . Y

Razón

Es una comparación entre dos cantidades.

Ejemplo: En un curso hay 12 mujeres y 20 hombres. Al representar estas cantidades en un par ordenado, éste es: 

( 12 , 20 )

FUNCIÓN 

Puedes escribir las entradas y salidas de una función como "pares ordenados", como (4,16).

Y una función se puede definir como un conjunto de pares ordenados :

Ejemplo: {(2,4), (4,5), (7,3)} es una función que dice que "2 se relaciona con 4", "4 se relaciona con 5" y "7 se relaciona con 3".

RELACIÓN CON LA MATEMÁTICA ( EJEMPLOS)

En matemáticas , es una pareja de objetos matemáticos, en la que se distingue un primer elemento y un segundo elemento. El par ordenado cuyo primer elemento es a y cuyo segundo elemento es b se denota como (a,b).

Los pares ordenados también se denominan 2-tuplas o vectores 2-dimensionales. La noción de una colección finita de objetos ordenados procede a generalizarse a mas de dos objetos , dando lugar al concepto de n-tuplas.

Ejemplo 1.

Si A = {2, 3} y B = {1, 4, 5}, encontrar tres relaciones definidas de A en B.

Solución 

El producto cartesiano de A x B está conformado por las siguientes parejas o pares ordenados:

A x B = {(2, 1), (2, 4), (2, 5), (3, 1), (3, 4), (3, 5)}
Y cada uno de los siguientes conjuntos corresponde a relaciones definidas de A en B:

R1 = {(2, 1), (3, 1)}
R2 = {(2, 4), (2, 5), (3, 4), (3, 5)}
R3 = {(2, 4), (3, 5)}


La relación R1 se puede definir como el conjunto de pares cuyo segundo elemento es 1, esto es, R1 = {(x, y) / y = 1}.
La relación R2 está formada por los pares cuyo primer componente es menor que el segundo componente, R2 = {(x, y) / x < y}
Y la relación R3 está conformada por todos los pares que cumplen con que el segundo componente es dos unidades mayor que el primer componente, dicho de otro modo, R3 = {(x, y) / y = x + 2}

Así, se puede continuar enumerando relaciones definidas a partir de A x B. Como se puede ver, la regla que define la relación se puede escribir mediante ecuaciones o desigualdades que relacionan los valores de x e y. Estas reglas son un medio conveniente para ordenar en pares los elementos de los dos conjuntos.

Ejemplo 2.

Dados los conjuntos C = {1, –3} y D = {2, 3, 6}, encontrar todos los pares ordenados (x, y) que satisfagan la relación
R = {(x, y) / x + y = 3}


Solución 

El producto cartesiano de C x D está formado por los siguientes pares ordenados 
C x D = {(1, 2), (1, 3), (1, 6), (–3, 2), (–3, 3), (–3, 6)}
Las parejas ordenadas que satisfacen que la suma de sus componentes sea igual a 3 son:

R = {(1, 2), (–3, 6)}

Toda relación queda definida si se conoce el conjunto de partida, el conjunto de llegada y la regla mediante la cual se asocian los elementos. En el ejemplo anterior, el conjunto de partida corresponde al conjunto C, el conjunto de llegada es el conjunto D y la expresión x + y = 3 es la regla que asocia los elementos de los dos conjuntos.

PROPIEDAD DE PARES ORDENADOS.

La propiedad característica de igualdad entre pares ordenados es su única propiedad relevante para su uso en matemáticas. Sin embargo, en teoría de conjuntos se construyen todos los objetos matemáticos a partir de conjuntos: números, funciones, etc. En este contexto, se utiliza una definición de par ordenado como un tipo particular de conjunto.

Mediante el axioma de extensionalidad y el axioma del par puede demostrarse que este término define un conjunto, con la propiedad característica del par ordenado.